La triangulation: un moyen simple pour s’orienter

1. Principe:

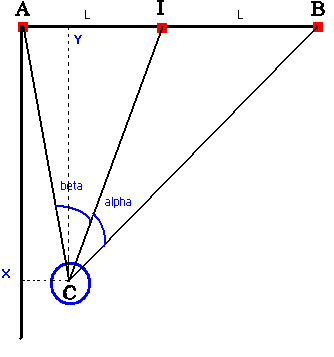
C'est une technique très élaborée,qui est très simple à mettre en œuvre et qui permet de se situer avec une très grande précision sur une carte. Le matériel nécessaire se réduit à une boussole de visée et une carte de la région dans laquelle on se trouve. La première chose à faire consiste à repérer dans les paysages des points caractéristiques bien visibles (pylône de télécommunications, phare, église, château d'eau…) et qui sont représentés sur la carte, il faut au moins deux points et idéalement trois. Une fois ces points repérés on mesure au moyen de la boussole de visée l'azimut de ces points caractéristiques on trace à partir de ces points sur la carte des droites dans la direction inverse de leur azimut respectif. Normalement l'intersection des droites correspond à la position exacte sur la carte ; il est préférable d'avoir trois points pour avoir une confirmation de l'exactitude, si les trois droites ne se croisent pas en un point mais forment un triangle c'est que les mesures ne sont pas parfaites mais on sait toutefois que l'on se trouve à l'intérieur de ce triangle. Ceci est illustré dans les deux schémas suivants.

La triangulation est utilisée de façon plus élaborée par les bateaux et les avions en utilisant non pas des repères visibles mais des radio phares ou des radio balises c'est ce que l'on appelle la radio navigation .L'appareil utilisé pour cela est un goniomètre.

2. Application:

Lors de randonnées,il arrive que l’on ait des difficultés à s’orienter malgré la présence d'une carte et d’une boussole. Cela peut se produire en montagne, en fôret partout où les sentiers sont inexistants. Alors, on a recours à la triangulation comme on l’a expliquée dans la partie précédente. La triangulation permet de situer avec une précision de quelques degrés, cependant il peut y avoir un décalage à cause de la déclinaison magnétique. En effet, la boussole indique la direction à l’aide d’azimuts exprimés en degrés. Mais pour que ceux-ci soient exacts, il faut tenir compte de la déclinaison magnétique. Qui est le plus souvent indiqué dans la marge de droite d’une carte topographique. La déclinaison magnétique, calculée pour le centre de la carte, fluctue chaque année (croît ou décroît. Cette variation est aussi indiquée sur la plupart des cartes. Si la déclinaison est de 10 degrés vers l’Ouest dans une région, il faut alors ajouter 10 degrés au Nord magnétique indiqué par la boussole. Si la boussole indique 30 degrés, on doit lire 40 degrés. Si, par contre la déclinaison est de 10 degrés vers l’Est ,il faut soustraire alors 10 degrés à la valeur indiquée par la boussole et lire 20 degrés.Cependant cette déclinaison est négligeable, par exemple, lorsque l’on fait une petite randonnée en France.

Exemple de triangulation:

Viser le point A (un bosquet), et relever son azimut (17°) par rapport au nord magnétique Viser le point B (un château d'eau), et relever son azimut (87°) par rapport au nord magnétique Corriger les relevés pour intégrer la déclinaison magnétique, pour cette région et à cette date, la déclinaison est de +3°. Soit les angles (20°), et (90°) à reporter sur la carte. Tracer les deux droites, XA, et XB ayant respectivement un angle et avec le nord géographique. Pour vérifier et affiner vos mesures et tracés, viser le point C (un château d'eau), et relever son azimut (157°). Corriger le relevé pour intégrer la déclinaison magnétique, soit l'angle (160°) à reporter sur la carte.


3. la triangulation d'un point de vue mathematique

• Quelques rappels géométriques

Pour résoudre ce problème géométrique, quelques relations vont nous servir:

FORMULE D´AL-KASHI

Dans le triangle quelconque ABC, on a les relations suivantes:

1. L² = CB² + CI² - 2CB.CI.cos()
2. L² = CI² + CA² - 2CI.CA.cos()

FORMULES DES SINUS

L/sin() = CI/sin(B)

L/sin() = CB/sin(A)

FORMULES DE PYTHAGORE

CB² = X² + (2L-Y)²

CI²= X² + (L-Y)²

CA² = X² + Y²

1. Etape1 :

Avec ces trois relations ,nous allons chercher à établir une relation donnant X et Y en fonction de et .

On sait que: sin (B)=X/CB et que sin(A)=X/CA en remplaçant dans la formule des sinus cela donne : CI.CB=L.X/sin() et CI.CA=L.X/sin()

On peut maintenant remplacer les produit CI.CA et CI.CB dans la formule d'Al-Kashi.

on obtient alors :

1. L²=X²+(2L-Y)²+X²+(L-Y)²-(2L.X/sin().cos())
2. L²=X²+(L-Y)²+X²+Y²-2(L.X/sin().cos()

En faisant (1-2) on trouve :

X=(2/T).(Y-L)

Avec T=(cos()/sin().(cos()/sin())

On obtient donc une première relation liant X Y et et .Il nous en faut alors une seconde.

2. Etape 2 :avec les tangentes

Soit ' l'angle tel que tan(')=Y/X et ' l'angle tel que tan(')=2L-Y/X

On a (' + ' )=( + )

En prenant en considération la relation tan(a + b) =(tan a +tan b)/1-(tan a. tan b)

On peut obtenir alors tan ( +)=(2X.L)/(X²-Y(2L-Y))

3. Etape3 :

Il suffit d'injecter X trouvé à l'étape 1 dans la formule précédente et on obtient :

a.Y²+bY+c=0

avec a=(4+T²)^(t/T)

b=(-2L/T²).(4+T²).t -4L/T

c=((4.L².t)/(T²))+(4L²/T)

t= tan ( +)

T=(cos( ) /sin())-(cos()/sin())

Cette équation du second degrés se résout par la méthode classique du discriminant ,on obtient alors une ou deux valeurs pour Y ;puis en remplaçant dans le résultat de l'étape 1 ,on trouve un deux couples pour X.

Remarque : le couple valide est celui pour lequel X et Y sont positif. Cas particulier :les formules précédentes ne s'appliquent pas dans le cas où = (division par zéro ) en effet dans ce cas ,on peut affirmer que Y=L et Tan()=Y/X d'où X= tan()

Conclusion:

Pour se repérer on connait maintenant les angles et et notre position(X,Y)

Vous êtes ici : accueil > les systèmes classiques de repérage > la triangulation